Well, maybe not "all", but a decent start...

Our host, Pythagoras (Image: World History Encyclopedia)
Tuning is surprisingly complicated.
We hear 2X a frequency as its octave (or 2nd harmonic). It may seem odd that we hear 40 to 80Hz as an octave and also hear 1,000 to 2,000Hz or 5,000 - 10,000Hz as an octave, but it's how we hear. It's logarithmic. We perceive volume the same way. We are what we are. So what does it mean?
Well, in our musical scale, all the intervals have ratios; we probably already know an octave is 2:1.
The others are:
1:1 Unison
2:1 Octave
3:2 Perfect Fifth
4:3 perfect Fourth
5:3 major 6th
5:4 major 3rd
8:5 minor 6th
6:5 minor 3rd
If you were to tune an instrument using these intervals, it is called "Just Intonation". It should work, right? Well, except for the logarithmic thing above. What happens is if you tune this way using the root, the 4th and 5th of the scale is it will sound pretty great in that key, but fall apart as you move away from that home key. Chords with flats or sharps will also be a problem. Your octaves won't line up either.
edit: I spoke to someone the other day who mentioned that this still doesn't make sense - the whole "log" thing.
Try this:
If every interval (2:1, 4:3 etc) was the same as the frequency intervals, this would work. The issue is that going 20hz to 40Hz is an octave, and so is going from 10,000-20,000. Every single increment up or down is slightly bigger (or smaller) than the prior increment. It just doesn't work in a way that is linear. It's like compound interest payments if that is any easier.
You have $100, you earn 5% on it and at the end of yer 1 you have $105. At the end of year 2 you have 5% of 105, and so on. It builds, and so to our tones.
But we're skipping a little ahead now.
Here is a quick table I made, pretending that if we take that first interval from A to Bb and just use it as every semi-tone lets see where we wind up:
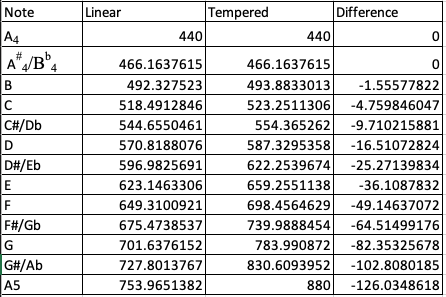
That initial step is ~26.16 Hz. If we keep using that frequency interval, our notes go flat at a faster and faster rate. It doesn't work because we don't hear changes in pitch linearly - we hear them logarithmically. Every octave is 2X the prior one. Every semi tone's frequency needs to be 1.055946...times the prior one. (see below) The choice of that first "tempered" interval was arbitrary, just to show how the math does not work out.
This has been a problem as long as we have played music on instruments, which is a really, really long time. [aside: Some scientists think the first instrument was a Neanderthal flute that is 60,000 years old. (https://www.nms.si/en/collections/highlights/343-Neanderthal-flute#) ]
One early solution was to tune using the maximum number of perfect 5ths (3:2 ratios) which yields something called the Pythagorean scale (named after, you guessed it, the triangle guy). Pythagoras is credited with figuring out that halving the length of a musical string would cause the musical pitch to rise to an octave. He also is credited with discovering that stopping a string 2/3 along its length would yield a perfect 5th, and stopping it 3/4 along its length would yield a perfect 4th. These are called harmonic ratios. While you would add musical intervals, you need to multiply harmonic ratios. Pythagoras figured out that by combining a perfect 5th and a perfect 4th you would make an octave.
You can try to tune with these harmonic ratios, but when you are done you miss the original note by an interval that became known as the 'Pythagorean comma'. Pythagorean tuning has the same issue as Just Intonation; it sounds good in its home key but gets worse as you move away and flats & sharps sound slightly out.
Where we eventually settled was something called "Equal temperament" which was invented in China and Europe independently around the years 1584-5. (more here: https://en.wikipedia.org/wiki/Equal_temperament#: )
We divide each octave into 12 pieces for our 12 semitones, and each semi-tone (adjacent notes) are derived from the prior one by multiplying it by the 12th root of 2.
Why?
Well our chromatic scale has 12 notes, and the 12th root of 2 is what you multiply 12 times to get the octave. (eg: the 2:1 ratio) Every semitone is all sharing the out-of-tune-ness because of this. We have just spread it evenly. Amortized it. All of your semitones are off, by design.
Another way to think of it is they drew a line in the sand around the octaves. The octaves are always right (hold that thought), and everything between them is equally sharing in the "off-ness'. This is because the octaves (any and all octaves) keep their 2:1 "Just" ratio. We backed into that by using that 12th root of 2. We made it work, on paper (and close enough for Jazz, lol)
A third way to think about came in by way of Brian Capleton's exhaustive article (link below) although this one confuses me: "Alternatively, we could look at this as dividing the octave into 12 equally sized semitones, which happens to produce tempered perfect fifths that are narrower than their harmonic size, by 1/12 of a comma, and tempered perfect fourths that are wider by 1/12 of a comma."
On the plus side, it doesn't really get worse changing keys or adding sharps and flats. But it probably explains a bit of the heartburn around tuning and intonation. You tune your guitar to play a perfect E major chord but now a C major sounds off. At least there is a logical reason now. You aren't crazy; just human.
DANGER: MATH AHEAD
The 12th root of 2 is 1.059463094359295
So a musical 5th is 1.05946 to the 7th power (7 semi-tones in a musical 5th) which is slightly flatter than 3/2 (the "Just" ratio above). And so on. You can use this to calculate all of your semitones. You can find tables and lists online or make a spreadsheet. Or just play your guitar.
This out of tune-ness extends to our instruments of course. Your guitar is going in and out of tune as you move up the neck. Test this out with your tuner. Ain't life grand?
There are various tuning adjustments that can be made here, such as sweetening. You can tune to specific keys in Just Intonation for example. One of the only major artists I am aware of who uses something like this is James Taylor; his tuning is below. Nice strobe tuners can handle a variety of sweetening and custom tunings so you can take this as far as you like. You can program tunings in and store them. Eddie Van Halen apparently sweetened his tuning as well, (here: https://www.petersontuners.com/inTune/Eddie-van-Halen)
James Taylor's tuning: "c" denotes a "cent" which is 1/100th of a semitone. -12c denotes 12 cents flat from tempered pitch. He goes on to explain in this video that he is correcting for the use of a capo and that the bass strings ring sharp otherwise: https://youtu.be/V2xnXArjPts
E (-12c)
A (-10c)
D (-8c)
G (-4c)
B (-6c)
E (-3c)
Acoustic or Electric Guitar is usually tuned (high to low)
1 (E) 329.63 Hz E4
2 (B) 246.94 Hz B3
3 (G) 196.00 Hz G3
4 (D) 146.83 Hz D3
5 (A) 110.00 Hz A2
6 (E) 82.41 Hz E2
Singers can, of course, work around it, as can instruments like Trombones, fretless instruments and so on. But some instruments have fixed pitches. Orchestra players may have to adjust their own intonation to match other instruments at times.
Inharmonicity in Guitar Strings
Now that we're experts at Equal Temperament, we can withstand a wrench in the works. There is a thing called Inharmonicity. We know that strings vibrate, and we've said that they have harmonics that are nice equal ratios (2x, 3x, etc) but this is not actually true. (and i have bad news about Santa!) Strings don't always do what we expect. And the reasons why can vary. Inharmonicity is where the harmonics are not nice equal ratios of the fundamental, they are off. Hitting or plucking strings makes it worse; bowing helps reduce it. Strings players, take a "bow", lol.
I became aware of this reading a response on Quora where a Piano tuner was writing about why Pianos have stretched octaves. It is because of inharmonicity. They tune by the 2nd harmonic - which if you think about it makes a lot of sense - you play middle C, (C4) and then you go to tune C5 (the next C up) the fundamental of which is the 2nd harmonic of C4. You do that because we often tune by beat frequencies - the pulses you hear when two pitches are very close. If you tuned dead on to the fundamentals, the harmonics would be beating against each other and it would not sound very good. So you tune to the octave to stop it from beating. This effect, inharmonicity, is partially a function of strings, and partially a function of how we make sound with strings.
At its root, inharmonicity is caused by stiffness in the string which relates to the string material itself. This is different than tension, which is a little confusing. We're really talking about the Young's modulus of the string material. We can measure this using test gear or even our tuning pegs to see how the length changes as we change the pitch. (one such paper is here: https://publicwebuploads.uwec.edu/documents/Musical-string-inharmonicity-Chris-Murray.pdf) We see how much tension it takes to come to pitch and then how much we have to stretch to get to other pitches. It also relates to the mass of the string. From the Wikipedia page:
"An ideal, homogeneous, infinitesimally thin or infinitely flexible string or column of air has exactly harmonic modes of vibration.[1] In any real musical instrument, the resonant body that produces the music tone—typically a string, wire, or column of air—deviates from this ideal and has some small or large amount of inharmonicity. For instance, a very thick string behaves less as an ideal string and more like a cylinder (a tube of mass), which has natural resonances that are not whole number multiples of the fundamental frequency."
This is intuitive if you take the extreme case - we hit a pipe with a hammer. It is going to "ring" at whatever frequency it naturally wants to. As you reduce the mass, the tension you put on it will have more and more influence. Thinner gauge strings should (in theory) intonate better. (has anyone seen a study? Is going from 10 down to 8 or 7 worth it?)
We have wound strings to help balance out tension, and in fact they are less likely to be inharmonic than solid strings. (the plain string in the center can stay smaller) Old strings, strings that are dirty or rusty are also more likely to be inharmonic. Frets that are out of place, poorly set bridge saddles or nuts can also make this worse. The string is being caused to not vibrate from its center, but slightly off of that. The G string on the guitar is naturally the worst offender because it is the thickest unwound string. The bigger the string gets, the more it takes on its own natural frequency, like hitting a length of pipe with a hammer. That is essentially what they mean by "tube of mass".
The other thing, is the actual length of the string that is vibrating. This means that you can have different amounts of inharmonicity on different frets of the same string. The shorter the stopped length is, the greater the inharmonicity. It will generally make the stopped note sound sharp. Basses have longer scales with wound strings in part to help address inharmonicity.
And as an aside, you should now realize that any guitar player who claims to be using heavy gauge piano strings is probably either lying or on something. They would not only be very hard to play but also would not play in tune. Reach inside a piano (ask first...) and feel how tight those strings are. They are much stiffer.
Falseness in Guitar Strings
You may notice a single string beating on its own as you tune it. This is called 'false beating'. You may not be able to hear it on a guitar, nor will you be able to stop it. But any other interval that includes this string will include this beating.
I had a really pretty '79 Ash bodied Strat originally that I wound up getting rid of because of the weird beating that came out of my chords. The neck was completely re-done by one of the best in the business, so I know the nut, frets and set up were right. It had these beats (like bad IMD) before and after the work. Doing double stops was bad enough; and whole chords just never rang properly. Was it something with the bridge? The wood? I don't know. My yellow strat doesn't do it.
A Tuning Approach to address both equal temperment & inharmonicity (Brian Capleton)
I am including Brian's approach here as 1) his site is no longer available and 2) it is a thoughtful approach that may help someone out. I have edited down his description to just the steps to make it simpler to follow.
1. Tune A(5) to another instrument or using a tuning fork.
Now we are going to take into account the effects of stopping on the 2nd fret, that may be caused by inharmonicity or fret/neck error.
2. Stop the A string on the 2nd fret and tune the B string to it. This is a B-B octave. Now test the C# on the B string, 2nd fret, against the open A. This is a major tenth A-C#. This will compete with the previous interval, the B-B octave. The tenth wants the B string to be lowered, whilst the octave wants it to be raised.
To have the tenth beatless would require the B-B octave to be beating narrow, unacceptably.
To have the B-B octave absolutely beatless, will require the tenth A-C# to be beating fast, wide.
You must decide where the right compromise falls, but you must expect to have perhaps 6 beats per second in the tenth A-C#, because it is intended to be an equally tempered interval, with a reasonably fast beat rate. The octave, on the other hand, does not "want" any beating. It may have to contain very slight beating in order to prevent the tenth A-C# from being unpleasantly fast beating, depending on how badly the strings stop sharp on the 2nd fret.
Next, we are going to take into account the effects of stopping on the 3rd fret, that may be caused by inharmonicity or fret/neck error.
3. Tune the D string an octave below the D stopped on the 3rd fret of the B string. Check the tuning of fifth between the E on the 2nd fret of the D string, and the open B string. This will compete with the previous interval, the D-D octave.
To have the octave beatless, will require the fifth to beat narrow.
To have the fifth beatless, will require the octave to be beating wide.
You must decide where the right compromise falls, but you must expect to have perhaps 1 beat per second in the fifth E-B because it is intended to be a narrow, equally tempered interval, with a slow beat rate.
4. Tune the top E string an octave above the E stopped on the 2nd fret of the D string.
Check the twelfth between the open A string and the open top E string. You must expect this to be very slow beating narrow, because it is a tempered interval.
Check the fifth between the open B string and the F# on the 2nd fret of the top E string. You must expect this to be very slow beating narrow, because it is a tempered interval.
Only compromise the octave if strictly necessary to overcome beating too fast in the twelfth and the fifth.
If the octave is fine, and the other intervals do not appear to be slow beating, this is fine.
5. Tune bottom E(6) two octaves below the top open E string.
Check with the E on the 2nd fret of the D string.
Check the twelfth with the open B string.
6. Tune the G string.
First, tune the octave from the A string to the G string stopped on the 2nd fret.
Next, check the major tenth from the bottom E string to the G# on the first fret of the G string. You must expect this to beat wide, because it is a tempered interval.
Next, check the fourth from the open G string to C stopped on the first fret of the B string. If this is too fast, you will have to raise the G string, re-checking the other intervals as you go.
Check also the fifth from the A on the G string's 2nd fret to the open top E string. You must expect this to beat fairly slowly narrow, because it is a tempered interval.
The open G and B strings should give a major third beating wide with about 8 beats per second. If this is too fast, the previous tuning was not as good as it could have been.
The open sixth G to top E should be a little faster than the G-B, and the open sixth D-B should be a little slower.
If this method is used, and the compromises are well made, the result should be optimal for the particular guitar being tuned. It works even on cheap guitars.
Tuner Basics
Tuners are not all the same. The reason you see so many stobe-style tuners backstage at big shows is because they are more accurate. This is essentially because they do not need a "null" - they are infinitely adjustable. The strobe disk spins in front of a lamp and you can visualize minute changes in pitch over time. Digital tuners need a null to make the indicator LEDs light up; the reality is that most instruments are not going to settle on that 1 frequency that is perfectly "in tune", they are going to vary a bit. There is a longer explanation here (turn to page 27: https://www.petersontuners.com/media/pdf/490%20Instruction%20Manual%20English%20Rev2.pdf ) And the better tuners will be accurate enough to help you set your own intonation and also store custom tunings if you decide you want to pursue some. I found a used Peterson 490 on ebay and it paid for itself in a couple of weeks.
Tuners however accurate are about getting the numbers (as opposed to the sound) right, but once you have figured out which adjustments sound best on your instrument and with your music, you can have a repeatable process.
Tunings
One of the great things about the Guitar is it can tolerate a lot of different tunings. And people have come up with lots of interesting tunings for them. Jerry Garcia famously did not learn a formal tuning at first and so taught himself through what are called "open tunings". Lots of other players have used them of course; many famous blues players, and also rock players like Jimmy Page & Paul Westerberg have taken advantage of them. You can get very different chord voicings out of them and give your playing a different sound. Ry Cooder famously showed Kieth Richards the open G tuning when they were recording "Sticky Fingers" and the rest is history. Kieth just leaves off the low "E" string altogether.
The BeeGees used open D among others (ex: Massachusetts) There is an easy video lesson here with good guitar close ups: https://youtu.be/6QtbgZOq1FY
A great way to thicken out an acoustic track is to pair a standard tuned guitar with an open tuned guitar, which is just what they do in "Massachusetts". Or pair the standard tuned guitar with a capo'd guitar. "September Gurls" by Big Star is using a pair of electric guitars, both capo'd at different frets (2nd & 7th) but in standard tuning to give the whole song a different vibe. Bands like Sonic Youth have gone to extremes, gigging with lots of different guitars in different tunings to craft their sound. See http://www.sonicyouth.com/mustang/tab/tuning.html for more on their tunings.
Here are a bunch of common ones to try out and some songs you may know that use them:
Standard E-A-D-G-B-E
DROP D D-A-D-G-B-E (Hash Pipe - Weezer, Dear Prudence - Beatles)
DOUBLE DROP D D-A-D-G-B-D ("Cinnamon girl" - Neil Young)
OPEN D D-A-D-F#-A-D ("Massachusetts" - The BeeGees)
OPEN Dm D-A-D-F-A-D ("Tunnel Of Love" - Dire Straits)
OPEN A E-A-C#-E-A-E ("Alex Chilton" - The Replacements
OPEN A (ALT) A-C#-E-A-C#-E
OPEN A (HAWAII) E-A-E-A-C#-E
OPEN Am E-A-C-E-A-E
OPEN C C-G-C-G-C-E ("Question" - The Moody Blues)
OPEN C6 C-A-C-G-C-E ("Friends" - Led Zeppelin)
LAP STEEL C6 C-E-G-A-C-E (Hawaiian / Country slide)
LOW C C-G-D-G-B-D
OPEN G D-G-D-G-B-D (Delta Blues, Alan Sparhawk - Low)
OPEN G DOBRO G-B-D-G-B-D
G MODAL D-G-C-G-C-D ("The Rain Song" - Led Zeppelin)
OPEN G6 (ALT) G-B-E-G-B-D ("Sleepwalk" - Santo & Johnny)
OPEN G6 D-B-G-E-B-G
D MODAL D-A-D-G-A-D ("Kashmir" - Led Zeppelin)
HALF STEP DOWN D#-G#-C#-F#-A#-D# (Hendrix, EVH, SRV, U2, Kiss, etc)
WHOLE STEP DOWN D-G-C-F-A-D
DROP C C-G-C-F-A-D
OPEN E E-B-E-G#-B-E (She talks to angels - Black Crows)
DROP B B-F#-B-E-G#-C#
NEW STANDARD C-G-D-A-E-G (A Robert Fripp / Crafty guitar thing)
OPEN Cm C-G-C-G-C-D#
OPEN Em E-B-E-G-B-E
OPEN Gm D-G-D-G-A#-D
STANDARD B B-E-A-D-F#-B
STANDARD C C-F-A#-D#-G-C
"Magic Man" E-A-D-G-D-G (By Heart, thanks Rick Erickson!)
You can go even farther, as Ricky Wilson did in the B52s (tunings from Gearslutz bbs post). He didn't really pay attention to a chord or key, preferring instead to tune things all around, or even remove strings to come up with riffs.
Planet Clair E-A-D-X-B-B (X indicates no string)
Rock Lobster C-F-X-X-F-F
Private Idaho E-B-X-X-B-B
NASHVILLE Standard tuning, (EADGBE) but using only the high strings from a 12 string set tuned to their correct pitches as if they whole set was in place. (Ex: the intro to Wild Horses - Stones or Here Comes a Regular - Replacements)
Finally, there is a cool site that is trying to collect open tunings and the songs they are used on.
Background:
How our scale works: https://en.wikipedia.org/wiki/Equal_temperament
Pythagorean Comma: https://en.wikipedia.org/wiki/Pythagorean_comma
Guitar string tension: https://www.daddario.com/the-lesson-room/guitar/acoustic-guitar/care/all-about-string-tension
Inharmonicity: https://en.wikipedia.org/wiki/Inharmonicity
Musical Scales and Frequencies: http://www.swarthmore.edu/NatSci/ceverba1/Class/e5_2006/MusicalScales.html
Tones and frequency: https://pages.mtu.edu/~suits/notefreqs.html
So Many Notes: https://en.wikipedia.org/wiki/Pitch_(music)
(about 120 audible notes in our equally tempered scale)
Alan Sparhawk Interview: http://www.silbermedia.com/qrd/archives/46alan.html
Guitar specifics found on www.amarilli.co.uk taken from Wayback machine snapshot of Jan 26, 2007. As referenced in above Wikipedia article on Inharmonicity. (c) Brian Capleton
Musical String Inharmonicity: https://publicwebuploads.uwec.edu/documents/Musical-string-inharmonicity-Chris-Murray.pdf
Comments